令和５年 問69
配列に格納されているデータを探索するときの、探索アルゴリズムに関する記述のうち、適切なものはどれか。
ア 2分探索法は、探索対象となる配列の先頭の要素から順に探索する。
イ 線形探索法で探索するのに必要な計算量は、探索対象となる配列の要素数に比例する。
ウ 線形探索法を用いるためには、探索対象となる配列の要素は要素の値で昇順又は降順にソートされている必要がある。
エ 探索対象となる配列が同一であれば、探索に必要な計算量は探索する値によらず、 2分探索法が線形探索法よりも少ない。
正解の理由
2分探索法は、データをあらかじめ決められた順番（例えば、小さい順、大きい順、五十音順など）にならべておき、探索の対象を半分ずつ狭めながらキーと比較していく探索方法です。
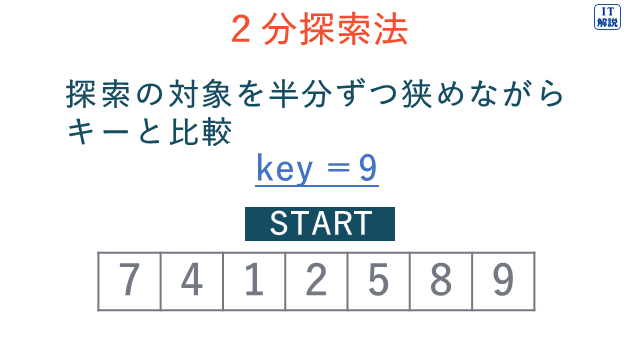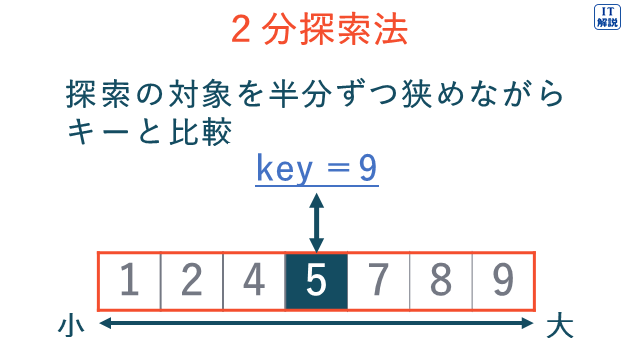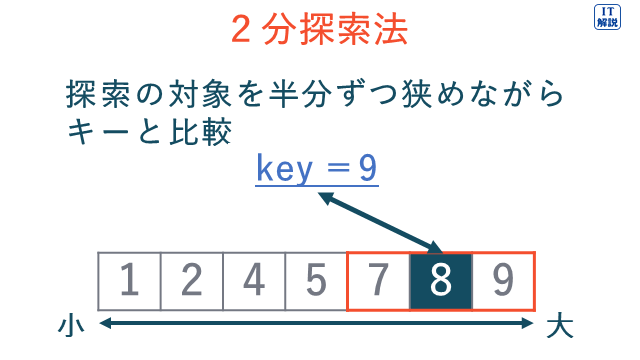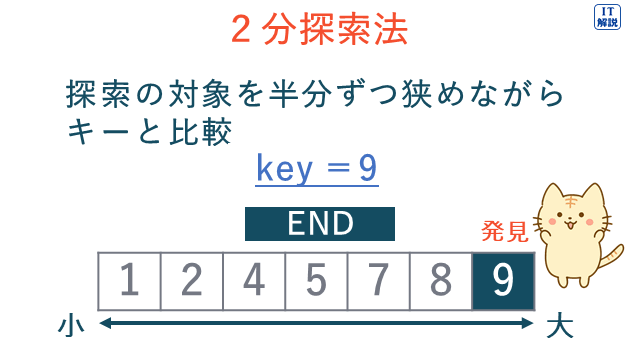
線形探索法は、データ列の先頭から順番にキーと比較していく探索方法です。
配列上に不規則に並んだ多数のデータの中から、特定のデータを探し出すのに適したアルゴリズムです。
(ソフト開発 平成19年春午前 問13より）
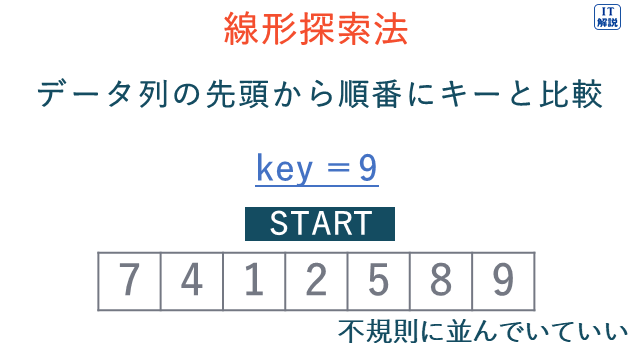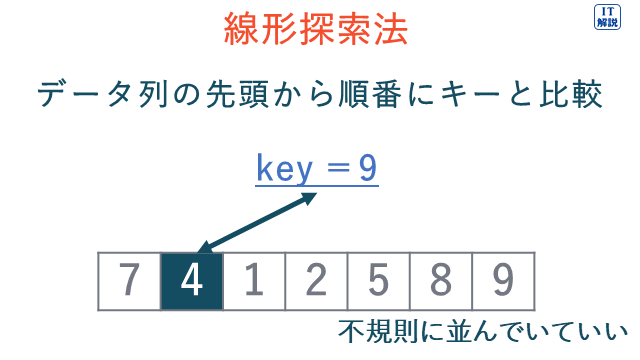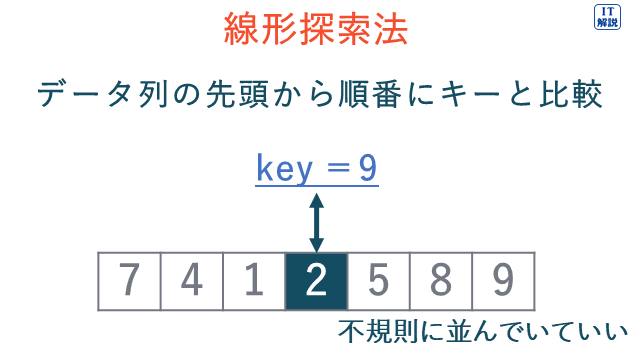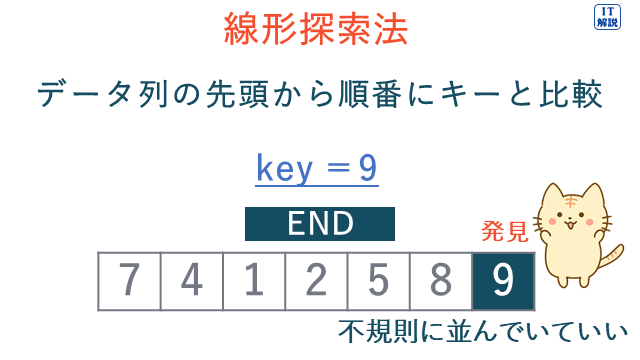
イ 線形探索法はデータ列の先頭から順番にキーと比較していくので、「線形探索法で探索するのに必要な計算量は、探索対象となる配列の要素数に比例する。」は、適切です。
よって、正解は イ です。
不正解の理由
ア 「探索対象となる配列の先頭の要素から順に探索する。」のは線形探索法です。
ウ 「探索対象となる配列の要素は要素の値で昇順又は降順にソートされている必要がある。」のは2分探索法です。
エ 目的の値が配列の先方にあると、２分探索法より、線形探索法の方が少ない計算量で目的の値が見つかることがあります。
「探索に必要な計算量は探索する値によらず、 2分探索法が線形探索法よりも少ない。」は、不適切です。
コメント