基礎 予想1
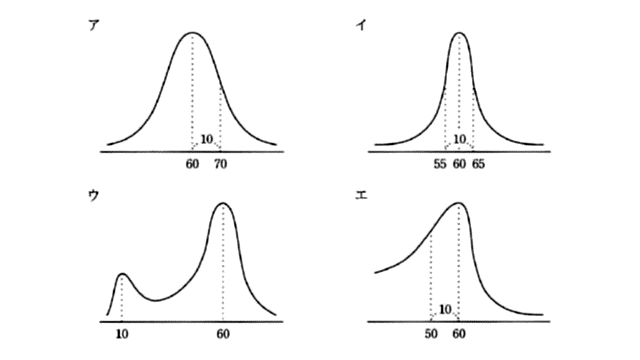
平均が60、標準偏差が10の正規分布を表すグラフはどれか。
出典:基本情報 令和元年秋午前 問5
正解の理由
正規分布は、どの値をとるか確実にはわからない変数について、値ごとに生じる確率を表したものです。
図のような釣り鐘のような形をしていて、平均値の生じる確率が最も大きく、平均値から離れるほど、生じる確率は小さくなっています。
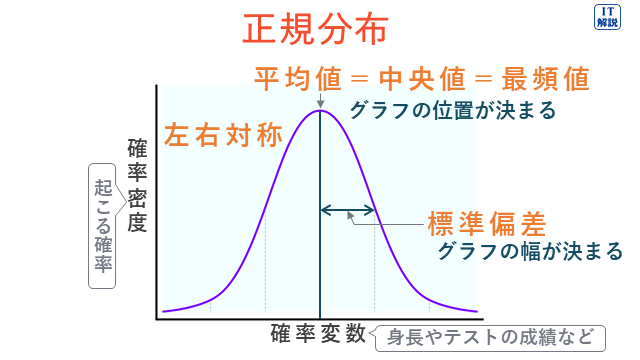
ア は、左右対称で、平均値の部分が最も高く、標準偏差の範囲が正しいです。
よって、正解は ア です。
基礎 予想2
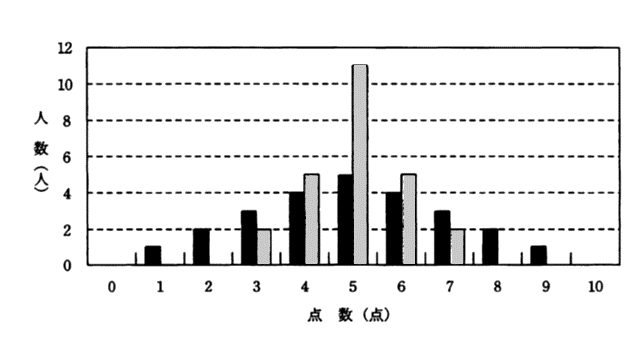
横軸を点数(O~10点)とし、縦軸を人数とする度数分布のグラフが、次の黒い棒グラフになった場合と、グレーの棒グラフになった場合を考える。二つの棒グラフを比較して言えることはどれか。
出典:ITパスポート 平成21年春 問80
正解の理由
分散は、データの散らばりの大きさを表す指標です。
下図のように、分散が大きいほどデータが散らばっていることを示します。
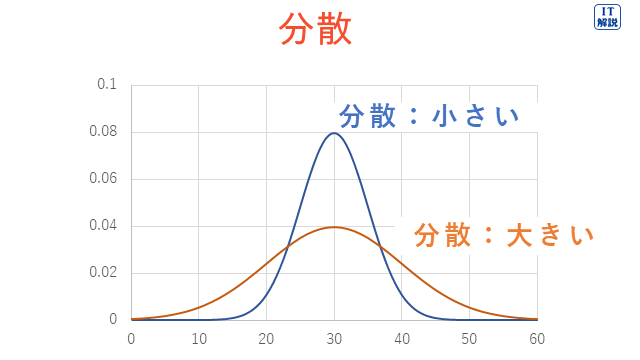
問題のグラフを見ると、グレーの棒グラフが、黒の棒グラフよりデータの散らばりが小さいので、正解は イ です。
基礎 予想3
相関係数に関する記述のうち、適切なものはどれか。
出典:応用情報 平成29年秋午前 問1
正解の理由
相関係数は、相関の強さを表す指標で、-1から1の間の値をとります。
2つの変量が正の相関関係にある場合、正の値をとり、負の相関関係にある場合、負の値をとります。
いずれの場合も相関が強いほど、1に近い大きな絶対値をとります。
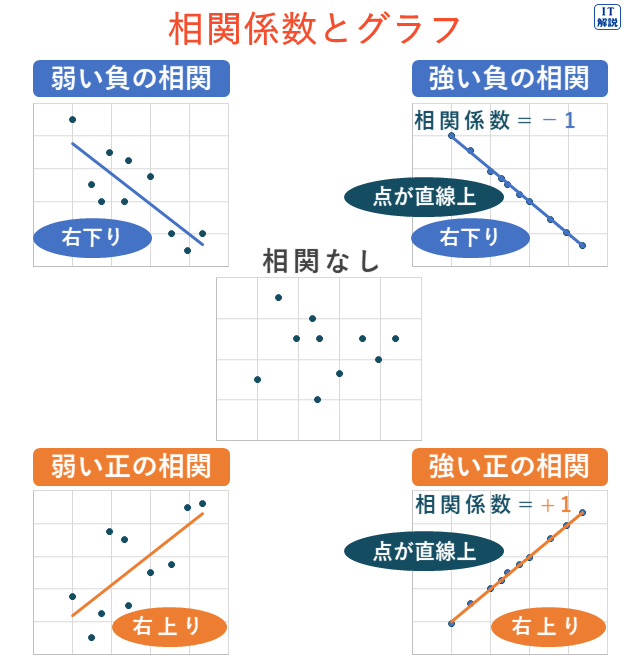
ア 「全ての標本点が正の傾きをもつ直線上にあるときは、相関係数が+1になる。」は、図の「強い正の相関」の場合に当たります。
よって、正解は ア です。
基礎 予想4
標本相関係数が-0.9、-0.7、 0.7、 0.9のいずれかとなる標本の分布と回帰直線を表したグラフのうち、標本相関係数が-0.9のものはどれか。
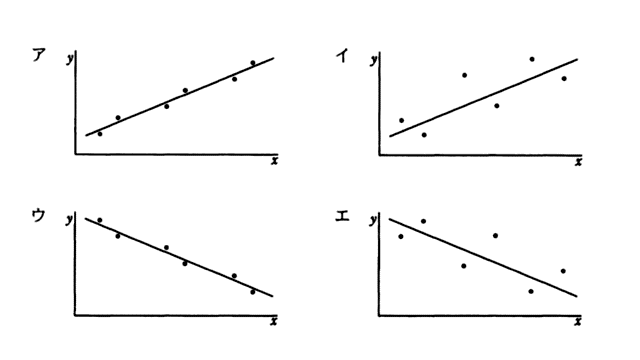
出典:基本情報 平成20年春午前 問8
正解の理由
相関係数は、相関の強さを表す指標で、-1から1の間の値をとります。
2つの変量が正の相関関係にある場合、正の値をとり、負の相関関係にある場合、負の値をとります。
いずれの場合も相関が強いほど、1に近い大きな絶対値をとります。

「標本相関係数が-0.9」とあるので、直線は右下がり、標本の分布はほぼ直線上になります。
よって、正解は ウ です。
基礎 予想5
数多くの数値の加算を行う場合、絶対値の小さなものから順番に計算するとよい。これは、どの誤差を抑制する方法を述べたものか。
出典:基本情報 平成17年春午前 問4
正解の理由
コンピュータ内部では、あらかじめ定められた範囲でしか数値を表現できません。 範囲を超える場合には、実際に近い値(近似値)を使います。 そのため、コンピュータで計算した値は、実際の値と異なる場合があり、実際の値と誤差が生じてしまいます。
情報落ちは、有効桁数が限られている場合、絶対値が大きい数と、小さい数の加減算で小さい数は計算結果に含まれなくなることで生じる誤差です。
そのため、誤差を少なくするためには、「数多くの数値の加算を行う場合、絶対値の小さなものから順番に計算するとよい。」です。
よって、正解は エ です。
不正解の理由
ア アンダフローは、計算結果の絶対値が、コンピュータが表現できる最小の値より、小さくなってしまうことを言います。
イ 打切り誤差は、 繰り返し計算を途中で打ち切って、近似値を求めた場合に生じる誤差です。
ウ けた落ちは、大きさが近い数同士の引き算で、有効桁数が減ってしまい生じる誤差です。
基礎 予想6
機械学習における教師あり学習の説明として、最も適切なものはどれか。
出典:基本情報 平成31年春午前 問4
正解の理由
教師あり学習は、正解データを与えて学習させます。
ウ 「正解のデータを提示したり、データが誤りであることを指摘したりする」とあるので、教師あり学習の説明です。
よって、正解は ウ です。
不正解の理由
ア 「個々の行動に対しての善しあしを得点として与える」とあるので、強化学習の説明です。
イ 「コンピュータ利用者の挙動データを蓄積し、挙動データの出現頻度に従って次の挙動を推論する。」とあり、正解データを与えていないので、教師なし学習の説明です。
エ 「正解のデータを提示せずに」とあるので、教師なし学習の説明です。
基礎 予想7
AIの機械学習における教師なし学習で用いられる手法として、最も適切なものはどれか。
出典:応用情報 令和元年秋午前 問4
正解の理由
教師なし学習は、正解データを与えないで学習させます。
ウ グループ分けの基準を与えていないので、教師なし学習の手法です。
よって、正解は ウ です。
不正解の理由
ア 「幾つかのグループに分かれている既存データ間に分離境界を定め」とあり、あらかじめ分離境界が与えられているので、教師あり学習です。
イ モンテカルロ法は、強化学習の手法です。「乱数を使って疑似データを作り、数値計算」が、強化学習の特徴である試行錯誤にあたります。
エ 回帰分析は、教師あり学習の手法です。「プロットされた時系列データ」が、教師あり学習の特徴である正解データにあたります。
基礎 予想8
AIにおけるディープラーニングの特徴はどれか。
出典:基本情報 平成30年春午前 問3
正解の理由
ディープラーニングは、大量のデータをニューラルネットワークで解析して、データの特徴を抽出、学習する技術です。
(ITパスポート 令和元年 問21より)
ウ 「ニューラルネットワークを用いて、人間と同じような認識ができるようにする」とあるので、ディープラーニングの特徴です。
よって、正解は ウ です。
不正解の理由
ア 「新しい知識を論理式で表現したルールに基づく推論の結果として、解を求める」は、ルールベースAIの特徴です。
イ ディープラーニングのアルゴリズムにもいくつかの種類があり、得意分野はそれぞれ違います。
「特定分野に特化せずに、広範囲で汎用的な問題解決ができるようにするもの」は不適切です。
エ ディープラーニングは、製造、金融など、さまざまな分野で利用されています。
「判断ルールを作成できる医療診断などの分野に限定される」は、不適切です。



コメント